Based on the “largest square in a histogram” problem (shown below), the goal is to analyze a binary 2D array consisting of ones and zeroes, and find the largest square section of the array that contains ones. This is useful for a number of tasks in statistics and image processing.
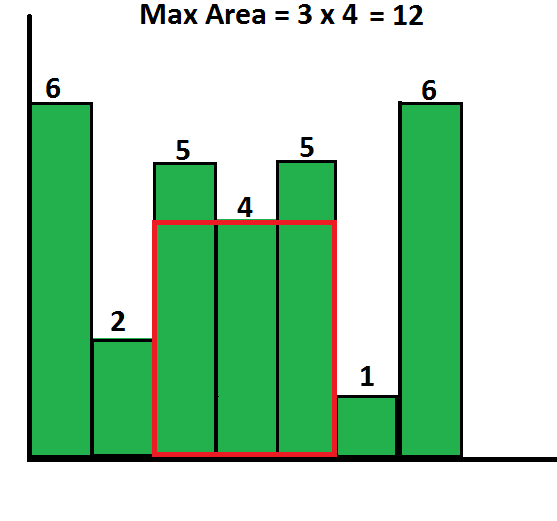
Largest rectangle in a histogram. (C) GeeksForGeeks.com – Shown under a FAIR USE exemption to the DMCA for works relating to public knowledge.
Using a “waterfall” incrementing operation, we arrive at the code shown below.
#include <stdio.h>
#include <time.h>
#include <stdlib.h>
#define bool int
#define R 20
#define C 20
void printMaxSubSquare(bool M[R][C]) {
int i,j;
int S[R][C];
int max_of_s, max_i, max_j;
/* Set first column of S[][]*/
for(i = 0; i < R; i++)
S[i][0] = M[i][0];
/* Set first row of S[][]*/
for(j = 0; j < C; j++)
S[0][j] = M[0][j];
/* Construct other entries of S[][]*/
for(i = 1; i < R; i++) {
for(j = 1; j < C; j++) {
if(M[i][j] == 1)
S[i][j] = min(S[i][j-1], S[i-1][j], S[i-1][j-1]) + 1;
else
S[i][j] = 0;
}
}
/* Find the maximum entry, and indexes of maximum entry
in S[][] */
max_of_s = S[0][0]; max_i = 0; max_j = 0;
for(i = 0; i < R; i++)
{
for(j = 0; j < C; j++)
{
if(max_of_s < S[i][j])
{
max_of_s = S[i][j];
max_i = i;
max_j = j;
}
}
}
printf("max_of_s:%d - max_i:%d - max_j:%d\n", max_of_s, max_i, max_j);
printf("\n Maximum size sub-matrix is: \n");
for(i = max_i; i > max_i - max_of_s; i--)
{
for(j = max_j; j > max_j - max_of_s; j--)
{
printf("%d ", M[i][j]);
}
printf("\n");
}
/* Print a prettier description of our result */
for (i=0; i<R; i++) {
for (j=0; j<C; j++) {
if ((i > max_i - max_of_s) && (i <= max_i) && (j > max_j - max_of_s) && (j <= max_j)) {
printf("# ");
} else {
printf(". ");
}
}
printf("\n");
}
printf("\n");
/* Print out the sum column */
for (i=0; i<R; i++) {
for (j=0; j<C; j++) {
printf("%d ", S[i][j]);
}
printf("\n");
}
printf("\n");
}
/* UTILITY FUNCTIONS */
/* Function to get minimum of three values */
int min(int a, int b, int c)
{
int m = a;
if (m > b)
m = b;
if (m > c)
m = c;
return m;
}
/* Driver function to test above functions */
int main()
{
int i, j;
const int bias = 2; /* Set to "2" for a 50/50 random chance; Higher bias
* means a greater chance of the value being set to
* true, and a larger sub-square being likely.
*/
bool M[R][C] = { 0 };
/*
bool M[R][C] = {{0, 1, 1, 0, 1},
{1, 1, 0, 1, 0},
{0, 1, 1, 1, 0},
{1, 1, 1, 1, 0},
{1, 1, 1, 1, 1},
{0, 0, 0, 0, 0}};
*/
srand(time(NULL));
for (i=0; i<R; i++) {
for (j=0; j<C; j++) {
M[i][j] = (rand() % bias)>=(bias-1)?0:1;
}
}
/* print overall square */
for (i=0; i<R; i++) {
for (j=0; j<C; j++) {
printf("%d ", M[i][j]);
}
printf("\n");
}
printf("\n");
printMaxSubSquare(M);
//getchar();
}
The best part about this, is by manipulating the “bias” variable, we can control the average number of ones versus zeros in the array, allowing us to see a number of different potential outcomes. With an “even” bias (ie: 50%), we see that the largest sub-square is often quite small.
0 1 0 1 0 0 1 1 1 1 1 0 0 0 1 0 1 1 1 0 1 1 1 1 0 1 1 1 1 1 0 1 1 1 0 0 1 0 1 1 0 1 0 0 0 0 0 0 1 0 1 0 1 0 1 0 1 0 1 1 0 0 0 1 1 1 1 1 1 0 0 1 0 0 1 1 0 0 1 0 0 1 1 1 1 0 1 0 1 1 1 1 1 0 0 1 1 0 0 0 1 1 1 0 1 0 1 0 0 0 0 1 0 1 0 0 1 1 1 1 0 1 0 1 0 1 1 0 0 1 0 0 0 1 1 1 1 1 1 0 0 1 1 0 0 0 0 0 1 1 1 0 0 0 0 0 0 0 1 0 1 0 0 1 0 1 1 1 1 0 1 1 1 0 1 0 1 1 0 0 1 0 1 0 0 1 1 0 1 0 1 0 1 1 0 1 1 0 1 0 1 1 0 0 0 0 1 1 0 0 1 0 1 1 1 0 1 1 1 0 1 0 0 0 0 0 0 1 1 0 0 0 0 0 1 1 1 1 1 0 1 1 0 0 0 0 0 0 1 1 1 0 0 1 1 0 1 0 0 1 1 1 0 1 0 1 0 1 0 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 1 0 1 1 1 0 1 0 1 1 1 1 1 0 1 1 1 1 0 1 1 1 0 0 0 1 0 0 1 1 1 0 1 0 0 0 0 0 0 0 1 1 1 0 0 1 1 0 0 0 0 0 1 0 0 1 1 0 0 0 0 0 1 0 1 1 1 0 0 0 0 1 1 1 1 0 0 1 1 1 1 1 1 1 0 1 0 0 0 1 1 1 0 0 0 1 1 1 0 1 1 1 1 0 1 1 0 1 1 0 1 0 0 1 0 max_of_s:2 - max_i:1 - max_j:7 Maximum size sub-matrix is: 1 1 1 1 . . . . . . # # . . . . . . . . . . . . . . . . . . # # . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 0 1 0 1 0 0 1 1 1 1 1 0 0 0 1 0 1 1 1 0 1 1 1 1 0 1 1 2 2 2 0 1 1 1 0 0 1 0 1 1 0 1 0 0 0 0 0 0 1 0 1 0 1 0 1 0 1 0 1 2 0 0 0 1 1 1 1 1 1 0 0 1 0 0 1 1 0 0 1 0 0 1 1 1 2 0 1 0 1 1 1 1 1 0 0 1 1 0 0 0 1 1 2 0 1 0 1 0 0 0 0 1 0 1 0 0 1 1 1 1 0 1 0 1 0 1 1 0 0 1 0 0 0 1 1 1 1 2 2 0 0 1 1 0 0 0 0 0 1 1 1 0 0 0 0 0 0 0 1 0 1 0 0 1 0 1 1 1 1 0 1 1 1 0 1 0 1 1 0 0 1 0 1 0 0 1 2 0 1 0 1 0 1 1 0 1 1 0 1 0 1 1 0 0 0 0 1 1 0 0 1 0 1 2 1 0 1 1 1 0 1 0 0 0 0 0 0 1 1 0 0 0 0 0 1 1 1 2 2 0 1 1 0 0 0 0 0 0 1 1 1 0 0 1 1 0 1 0 0 1 1 2 0 1 0 1 0 1 0 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 1 0 1 1 1 0 1 0 1 1 1 1 1 0 1 1 1 1 0 1 2 1 0 0 0 1 0 0 1 2 2 0 1 0 0 0 0 0 0 0 1 2 1 0 0 1 1 0 0 0 0 0 1 0 0 1 1 0 0 0 0 0 1 0 1 1 2 0 0 0 0 1 1 1 1 0 0 1 1 1 1 1 1 1 0 1 0 0 0 1 1 1 0 0 0 1 1 1 0 1 2 2 2 0 1 1 0 1 1 0 1 0 0 1 0
While with a modified bias (80% in the case below) we get much larger sub-squares.
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 max_of_s:14 - max_i:19 - max_j:18 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . # # # # # # # # # # # # # # . . . . . . # # # # # # # # # # # # # # . . . . . . # # # # # # # # # # # # # # . . . . . . # # # # # # # # # # # # # # . . . . . . # # # # # # # # # # # # # # . . . . . . # # # # # # # # # # # # # # . . . . . . # # # # # # # # # # # # # # . . . . . . # # # # # # # # # # # # # # . . . . . . # # # # # # # # # # # # # # . . . . . . # # # # # # # # # # # # # # . . . . . . # # # # # # # # # # # # # # . . . . . . # # # # # # # # # # # # # # . . . . . . # # # # # # # # # # # # # # . . . . . . # # # # # # # # # # # # # # . 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 1 2 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 1 2 3 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 1 2 3 0 1 2 3 4 5 5 5 5 5 5 5 5 5 5 5 5 1 2 3 1 1 2 3 4 5 6 6 6 6 0 1 2 3 4 5 6 1 2 3 2 2 2 3 4 5 6 7 7 7 1 1 2 3 4 5 6 1 2 3 3 3 3 3 4 5 6 7 8 8 2 2 2 3 4 5 6 1 2 3 4 4 4 4 4 5 6 7 8 9 3 3 3 3 4 5 6 1 2 3 4 5 5 5 5 5 6 7 8 9 4 4 4 4 4 5 6 1 2 3 4 5 6 6 6 6 6 7 8 9 5 5 5 5 5 5 6 1 2 3 4 5 6 7 7 7 7 7 8 9 6 6 6 6 6 6 6 1 2 3 4 5 6 7 8 8 8 8 8 9 7 7 7 7 7 7 7 1 2 3 4 5 6 7 8 9 9 9 9 9 8 8 8 8 8 8 8 1 2 3 4 5 6 7 8 9 10 10 10 10 9 9 9 9 9 9 9 1 0 1 2 3 4 5 6 7 8 9 10 11 10 10 10 10 10 10 10 1 1 1 2 0 1 2 3 4 5 6 7 8 9 10 11 11 11 11 11 1 2 2 2 0 1 2 3 4 5 6 7 8 9 10 11 12 12 12 12 1 2 3 3 1 1 2 3 4 5 6 7 8 9 10 11 12 13 13 13 1 2 3 4 2 2 2 3 4 5 6 7 8 9 10 11 12 13 14 14
