Well, now that we can downsample an image and reduce its dimensions, it would be nice to be able to increase the dimensions of an image. When downsampling, we have a very simple task – throw away data (according to strict calculations of course).

When we want to increase image dimensions, we are basically expanding an image, and filling in “gaps” in rows and columns of the original image. For example, say we want to increase the width and height of an image by a factor of 4. We could simply “repeat/redraw” each row and column of the original image 4 times. Sample code and sample images are shown below.

%Import my original picture file

I = imread('trees_small.jpg','jpg');

%Convert image to grayscale (intensity) values for simplicity (for now)

I = rgb2gray(I);

%Determine the dimensions of the source image

%Note that we will have three values - width, height, and the number

%of color vectors, 3

[j k] = size(I)

%Determine how much larger we want the new image (should be an integer)

scale = 4;

%Declare and initialize an output image buffer

M = zeros(scale.*j,scale.*k);

%Generator the output image

for count1 = 1:scale:j.*scale

 for count2 = 1:scale:k.*scale

 for count3 = 1:scale

 for count4 = 1:scale

 M(count1+count3,count2+count4) = I(ceil(count1./scale),ceil(count2./scale));

 end

 end

 end

end

%Display the two images side-by-side for a few seconds, then close

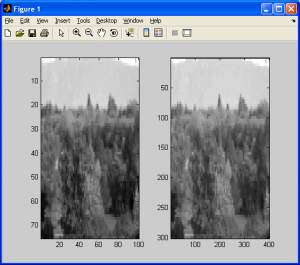
subplot(1,2,1); imagesc(I);colormap gray; axis tight;

subplot(1,2,2); imagesc(M);colormap gray; axis tight;

pause(4);

close all;

Upsampled image after cloning columns and rows

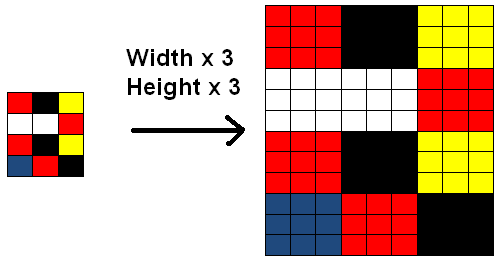
Interestingly enough, when both images are scaled side-by-side, they look identical. By duplicating entire rows and columns, we have not created any “new” data. The extra rows and columns are completely redundant, and do not provide any real improvement, nor do they provide data that we did not already have, leaving this approach completely useless for increasing the dimensions of images (at least so far as these tutorials are concerned). An example of increasing the width and height of an image by a factor of 3 is shown below to give a graphical demonstration of exactly what is happening.

Basic Upsampling by a Factor of 3

Another problem with this approach is that it only works when we want to increase the image dimensions by an integral factor (ie: 2, 4, 10), as it cannot deal with the case of image scaling by a fractional number (2.5, 10/3, etc). If we want to increase the dimensions of the image AND be able to overcome the shortcomings of the previous example, we need to interpolate image data – using mathematical produces to provide a reasonably accurate intermediate value between pixels. In the following subsections I will cover some of the most common approaches to increasing the dimensions of an image by interpolation.