In the past two parts of this section, we’ve covered two types of filtering so far: linear, and non-linear. In the case of linear filtering, we applied convolution masks to an image to blur it. This type of filter basically calculates a sum-of-products using a filter mask and a source image, which is a linear operation. In the case of non-linear filtering, we used median filtering, which takes a neighborhood of pixels, calculates the median value, and uses that value in the final result. This is obviously a non-linear operation.

Now we will cover a sort of hybrid model: adaptive filtering. One problem we have encountered with attempting to filter out salt & pepper noise and Gaussian noise is that when we are dealing with very “noisy” images, we tend to require larger filter masks to remove such large quantities of image noise. Although we can use arbitrarily large masks, the end result is that the larger the mask we use, the poorer the quality of the output image. What we would like is a means to determine if a pixel in a noisy image has been affected by the introduction of noise, and performing filtering on a conditional basis.

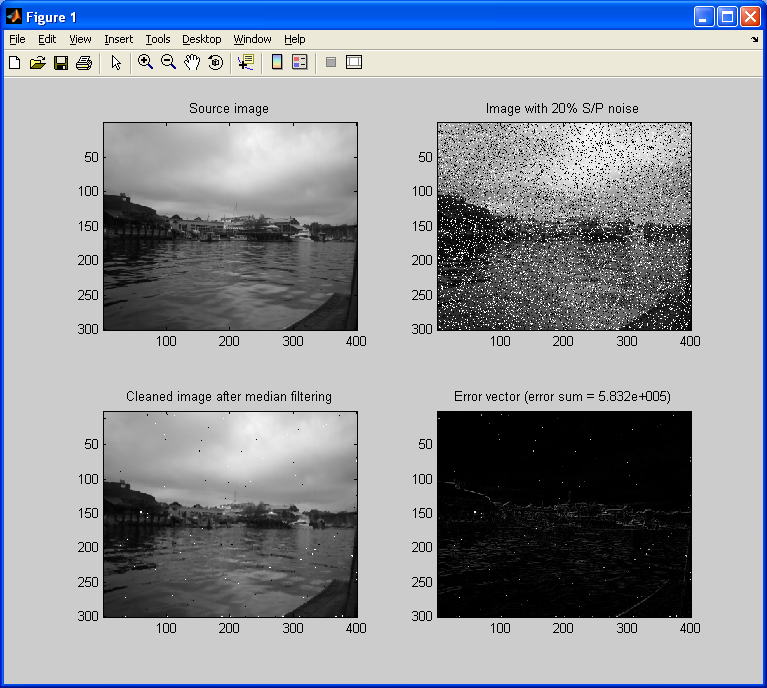
Although adaptive filters are a subject all of their own, I will present a simple adaptive filter I have designed for the removal of salt & pepper noise from an image. First, consider the example below, where I remove a considerable amount of salt & pepper noise from an image (20% added noise) using a 3×3 median filter.

20% Salt & pepper noise removal – 3×3 static median mask

The error vector/image above makes it clear that the filtered image is distorted compared to the original image. Most notably, it appears blurry, with sharp edges and fine details having been removed by some degree. Now, let’s make a simple modification to the code for a simple median filter. For each pixel in the source image, it will assess whether or not the pixel is considered to be a noisy pixel according to a simple contrast checking algorithm.

This algorithm will attempt to determine if the pixel under consideration is a statistical outlier compared to its surrounding/neighboring pixels. If it is considered to be a noisy pixel, then a median filter is applied to the neighborhood of this pixel, and the median value is used for the result to be stored in the output image buffer. If the pixel is not considered to be noisy, it is simply copied directly into the output image buffer, with no median mask applied at all.

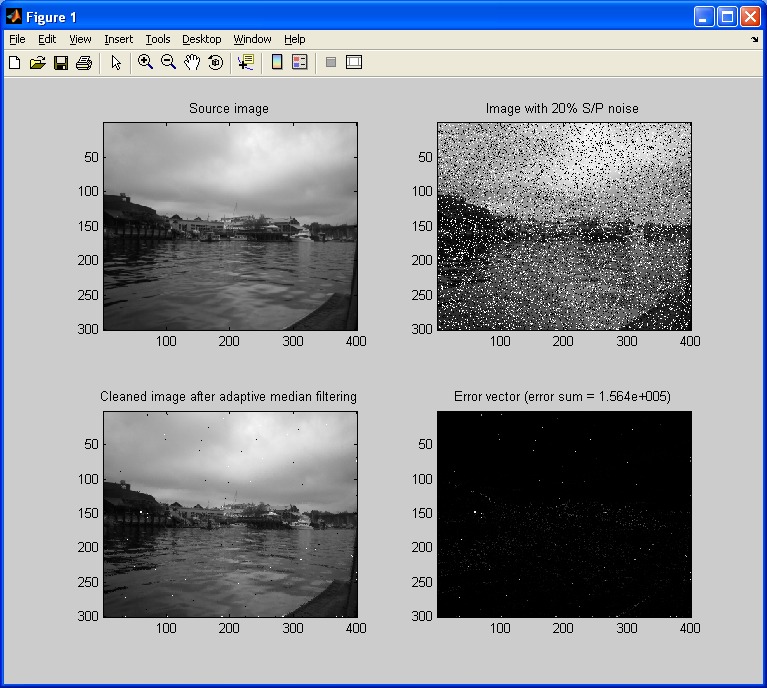
The images below will demonstrate this algorithm in action, and compare the quality of its output compared to that of a simple median filter.

20% Salt & pepper noise removal – 3×3 adaptive median mask

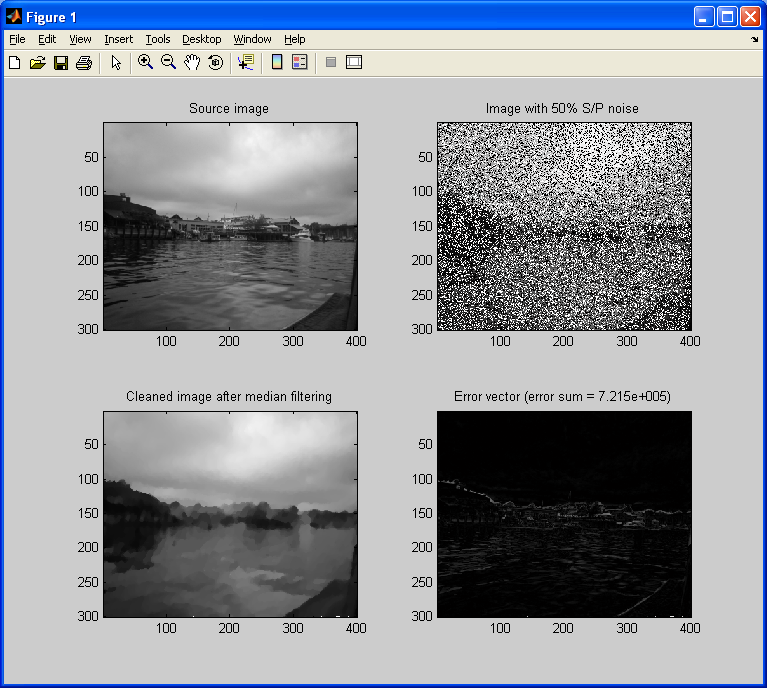
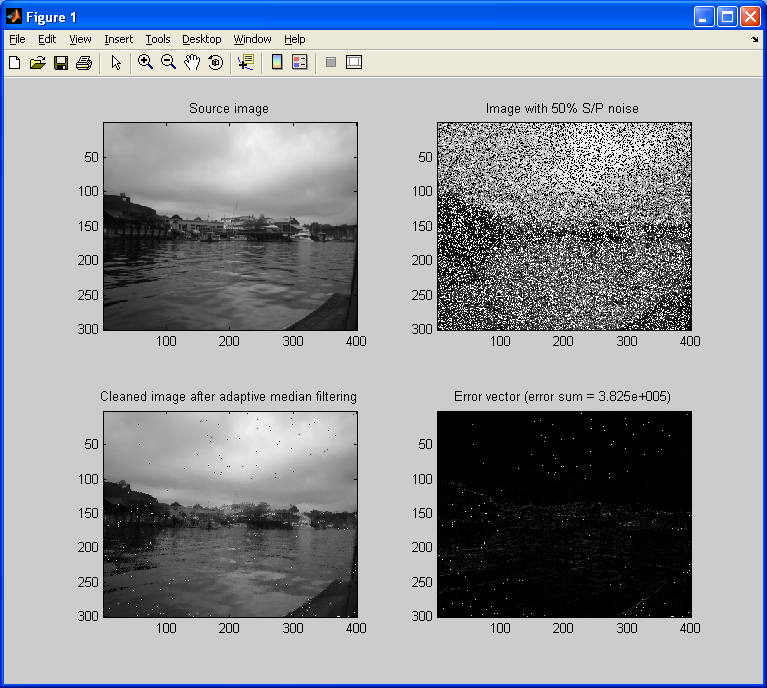
As we can see above, the adaptive method removes a significant amount of noise, without blurring the image. The error value (as shown in the title for the error vector/image) also decreases significantly (by nearly three-fourths) by using an adaptive filter over a static one. For completeness, I will perform this experiment again, but with 50% salt & pepper noise, and filtering using static/adaptive 7×7 median filters.

50% Salt & pepper noise removal – 7×7 static median mask

Notice how blurry the de-noised/cleaned image is after applying the static 7×7 median mask. All the fine lines, edges, and details have been lost.

50% Salt & pepper noise removal – 7×7 adaptive median mask

Although the reduction in error is only one-half, it is still a significant gain. Also, it is quite impressive that we have this clear an image despite approximately half of the pixels in the noisy image were basically complete garbage (pure noise). One may also notice that, interestingly enough, there some bright (salt) pixels in the middle of dark areas, and dark (pepper) pixels in the middle of a bright area. Shouldn’t the adaptive filter have removed such obvious statistical outliers, given that are salt/pepper (ie: extreme valued) pixels?

The answer to this is simple: there was so much noise in the original image, that there were random parts of the noisy image where the majority of the pixels in a 7×7 pixel neighborhood were salt/pepper pixels. So, for those particular 7×7 pixel neighborhoods, these pixels weren’t categorically statistical outliers. There is a simple way to deal with this though: run the filter on the image again (ie: multi-pass). We simply take the output image after applying the adaptive median filter, and run this result through the filter again. The loss in quality (in the case of this salt & pepper filter) incurred by running this filter for more than one pass is minimal, and will easily remove the remaining salt & pepper pixels.

Before concluding this topic, I will leave the reader with the code for my adaptive salt & pepper median filter, along with one important note: the execution time for the adaptive filter calculates a large number of statistics several times throughout its main logic loop. This means that it will take a considerably larger amount of resources (ie: RAM, computation time, etc) compared to the simple/static median filter. So, although we end up with a better result, it does come with a price.

%==========================================================================
function[A] = imgMaskMedAdaptive(src_matrix,dim_matrix)
% imgMaskMedAdatptive   -   Applies an adaptive median filter to a noisy
% source image
% src_matrix            -   the original image to copy and modify afterwards
% dim_matrix            -   is the dimension of the mask size
% (C) 2010 Matthew Giassa, <teo@giassa.net>  www.giassa.net
%==========================================================================
% Copy original image data to a temporary buffer
% and flatten to a 2D grayscale matrix
copy_matrix = src_matrix;

%Definitions
SALT_VALUE = intmax('uint8');
PEPPER_VALUE = intmin('uint8');

% Determine the dimensions of the source matrix
[x,y] = size(copy_matrix);

% Determine the dimensions to use for the median filter
a = dim_matrix;
b = dim_matrix;

% Error checking code
% Non-square mask matrix
if(a~=b)
 disp(sprintf('Mask matrix is not square!'))
elsif((a==0) | (b==0))
 disp(sprintf('Mask matrix has a singleton dimension!'))
elsif((a<3) | (b<3))
 disp(sprintf('Mask matrix is not at least 3x3!'))
elsif((a>=(x-1)) | (b>=(y-1)))
 disp(sprintf('Mask matrix dimenions are too large!'))
else
 % Pad the matrix edges so we don't lose data
 for j = 1:b
 [a_temp, b_temp] = size(copy_matrix);
 copy_matrix = vertcat(copy_matrix, copy_matrix(a_temp,:));
 copy_matrix = vertcat(copy_matrix(1,:), copy_matrix);
 copy_matrix = horzcat(copy_matrix, copy_matrix(:,b_temp));
 copy_matrix = horzcat(copy_matrix(:,1), copy_matrix);
 end
 % Re-read the new (padded) image size
 [x,y] = size(copy_matrix);
 % Generate a vector containing all elements of the mask matrix
 median_matrix = [];
 for k1=1+ceil(b/2):y-ceil(b/2)
 for k2=1+ceil(a/2):x-ceil(a/2)
 for k3=1:b
 for k4 = 1:a
 median_matrix = horzcat(median_matrix,copy_matrix(k2-floor(b/2)+k4,k1-floor(a/2)+k3));
 end
 end
 centrePixel = copy_matrix(k2,k1);
 average = mean(median_matrix);
 stddev = sqrt(var(median_matrix));
 %Two major conditions:
 %1-Is the pixel an extreme statistical outlier, ie: more than 3
 %times the standard deviation from the mean?
 %2-Is the pixel a salt/pepper pixel?
 if((abs(centrePixel-average)<3.0*stddev) && ((centrePixel == SALT_VALUE) || (centrePixel == PEPPER_VALUE)))
 result = median(median_matrix);
 else
 result = centrePixel;
 end
 copy_matrix(k2,k1) = result;
 median_matrix = [];
 end
 end

 % Trim the matrix edges so input resolution = output resolution
 for j = 1:b
 [a_temp, b_temp] = size(copy_matrix);
 copy_matrix(a_temp,:) = [];
 copy_matrix(:,b_temp) = [];
 copy_matrix(1,:) = [];
 copy_matrix(:,1) = [];
 end
end
%==========================================================================
%======= Complete
%==========================================================================

A = copy_matrix;